アメリカのコンプトンが行った、光電効果の拡張実験「コンプトン効果」である。以前説明したようにその結果は、光の粒子性を揺るぎないものとして証明したのであった。
ところが、ふたつめの出来事は、全く正反対の事象を示すものであった。なんと、電子は波である、と言い出した人がいたのだ。その人の名をド・ブロイという。ところで、アインシュタインは「光が粒子の性質を持つのであるなら、運動量も持つはずだ！」と考え、光子の運動量 p=h/\lambda （h:プランク定数、\lambda:光の波長）と予想をし、それがコンプトン効果によって証明されていた。そこでボーアは「陽子や電子が粒子であるなら運動量 p=mv を持つはずであり、また同時に陽子や電子が粒子と波との二重性を持つなら、光と同じように運動量 p=h/\lambda を持つであろうと考え、 mv=h/\lambda となり、以下のようになる。
ド・ブロイの物質波　 \lambda=\frac{h}{mv}
ちなみに光子の場合には質量をもたないので \lambda=h/mv にはならないのだ。これはあくまでも、陽子や電子の場合だ。そして、この式が、先ほどのボーアの式につながるのだ！
まず、電子は原子核の周りをグルグル回っている。その円の長さは 2\pi r だ。一方で、電子は波である！（と仮定している！）波ならば波長がある。波長を \lambda としよう。波には、高い部分と低い部分、山と谷がある。もし電子が円の長さ 2\pi r を1周して戻ってきたときに、この山と谷の位置がずれていたら円はつながらなくなってしまうのだ。また、別の説明をすると、山の位置と谷の位置が1周目と2周目でずれてしまうと波が弱くなり安定して存在することができないのだ。こうしてド・ブロイは、電子が波であると考えたとき、波の始まりと終わりが、円周上で一致するような波であると考えた。このためには、円周の長さを波長で割った値が割り切れる（つまり1、2、3、…）という整数になる必要がある。ではこれを式にしてみよう。 2\pi r=m\lambda である。ところで先ほど述べたように\lambda=h/mv であるから、代入すると、 2\pi r=nh/mv となり、さらに2\pi mvr=nh となる。　
これはボーアの式と同じになるのだ！　ボーア自身は電子を波と考えて式を作った訳ではないのだが、その後、電子を波と考えたド・ブロイによって、ボーアの式は電子を波と考えていると解釈できるようになったのだ！　そして逆にド・ブロイの考えは、ボーアの電子モデルによって支持されるようになったのだ。
電子が波であるということは、原子が波であるということだ。原子が波であれば原子から成り立つすべてのものは波なんだ。まさに、古典物理が崩れ去り、あらたな物理学「量子論」が誕生した瞬間である。

 第7章二重スリット実験

二重スリット実験

最初に、量子力学の二重スリット実験を 紹介 したいと思います。

電子が壁に向かって飛んでいます。 その壁 には二個のすきまがあります。 その電子は、壁に あたるか、あるいは、すきまをとおります。 すきまをとおった電子は、もうひとつの壁にあたります。 たくさんの電子がすきまをとおると、なにが起こるでしょうか？

壁にあたる電子の個数を増やすと、しま模様が 電子の分布となります。
なにが、このしま模様を作ったのでしょうか？ 実は、電子は波の性質をもっています。 二個のすきまをとおった波は強め合ったり弱めあったりします。 この現象は干渉と呼ばれています。 波の干渉が、そのしま模様を作りました。 この実験は「二重スリット実験」と呼ばれています。 私は、この結果をとても不思議だと思います。 電子は一個ずつ、すきまをとおります。 なぜ 干渉による、しま模様 を見ることができるのでしょうか？

なぜ干渉による、しま模様が作られるのか？

電子の波は次の関数で表現します。
Ψ (x )
この関数は波動関数と呼ばれ、プサイ・エックスと発音されます。 変数xは電子の位置を記述する実数です。 波動関数は、複素数の関数です。 波動関数は、電子の状態を記述します。
二重スリット実験で、電子には二つの経路があります。 一番目の経路は、右のすきまをとおる経路です。 二番目の経路は、左のすきまをとおる経路です。 右のすきまをとおった波の波動関数を ΨR (x ) と表現します。 左のすきまをとおった波の波動関数を ΨL (x ) と表現します。 これらの二つの波動関数 ΨR (x )とΨL (x ) を足し算します。
Ψ (x ) = ΨR (x ) + ΨL (x )
この足し算によって、干渉が発生します。 これを「重ね合わせの原理」といいます。 電子の観測確率P(x )は、波動関数の絶対値の2乗となります。
P (x ) = |Ψ (x ) |2
なぜ、電子の観測確率は、波動関数の絶対値の2乗なのでしょうか？
物理学者のファインマンは1965年に次のように述べています。
いまでもまだ、次のような質問をしようとする人がいるかもしれない。 "どうしてそんなことになるのか。法則の背後にかくされているからくりは何か" と。
法則の背後のからくりなどを発見した人は、これまでひとりもいない。 たったいま "説明" した以上のことを "説明" できる人はいない。 だれも、いまの状況をより深遠に表現してくれるひとはない。 上に述べた結果を導きうるようなより基本的な機構についてのアイディアを、 われわれはもっていないのである。
つまり、仕組みは「わからない」のです。  1951年のアインシュタインの言葉も引用します。
50年間も意識して問題をあたためながら、 私はまだ " 光の量子とは何か " という問題の答えに、 少しも近づいておりません。 もちろん今日では、誰もが答えを知っていると思っています。 しかしそれはみずからを欺いているにすぎません。
第8章 素粒子の寿命と質量
素粒子は寿命と質量をもちます。 電子は無限の寿命をもつと考えられています。 電子の質量は 0.5 MeVです。 一方、陽子は有限の寿命をもつと考えられています。 しかし、その寿命の長さは、まだわかっていません。 陽子の質量は約 940 MeVです。 もし、電子の質量を0.5gと仮定すれば、陽子の質量は約940gになります。
宇宙では、陽子が高速で飛んでいます。それらは宇宙線と呼ばれています。 その陽子が、大気中の原子と衝突し、いろいろな素粒子が生成されます。 素粒子の一部はタウ粒子とミュー粒子です。
タウ粒子の性質は電子と似ています。 タウ粒子の質量は約1800 MeVです。 もし、電子の質量を0.5gと仮定すれば、タウ粒子の質量は約1800gになります。 このタウ粒子の平均寿命は300フェムト秒です。1フェムト秒は1000兆分の1秒です。 タウ粒子は電子とニュートリノに崩壊します。
ミュー粒子の性質は電子と似ています。 ミュー粒子の質量は約100 MeVです。 もし、電子の質量を0.5gと仮定すれば、ミュー粒子の質量は約100gになります。 このミュー粒子の平均寿命は2マイクロ秒です。1マイクロ秒は100万分の1秒です。 もし、タウ粒子の平均寿命を約1000年と仮定すれば、ミュー粒子の平均寿命は7億年になります。 ミュー粒子は電子とニュートリノに崩壊します。
光子は2マイクロ秒で600m進みます。 ミュー粒子の平均寿命は2マイクロ秒であるため、600mも進まないはずです。 しかし実際には、6000m以上も進み、地表へ到達します。 特殊相対性理論の効果が、ミュー粒子の寿命をのばすためです。
素粒子が寿命をもつことは、とても不思議なことです。 ろうそくの寿命じゅみょうはそのロウの部分の長さで決まります。 でも、それぞれの素粒子の寿命は、初めから決まっているわけではないのです。 生まれて1000年たった素粒子も、7億年たった素粒子もまったく同じ素粒子なのです。 いいかえれば、自分が何才なのかまったく覚えてないわけです。
それぞれの素粒子そりゅうしは単位時間ごとに一定の確率で崩壊しています。 たとえば、素粒子は1秒ごとにサイコロをふって、次のように行動します。
  • その素粒子がサイコロをふり番号6を得た場合、その素粒子は崩壊する。
  • その素粒子がサイコロをふり番号6を得なかった場合、その素粒子は崩壊かいしない。
サイコロをふるという表現は比喩です。 しかしながら、素粒子は、どのようにサイコロをふるのでしょうか？ サイコロをふる時間間隔はどのくらいなのでしょうか？ 私は、その時間間隔はとても短いと考えます。 その時間間隔は時間の最小単位なのかもしれません。
このように、素粒子の崩壊に関しても、不思議なことがたくさんあるのです。
第９章量子力学の薄膜干渉
量子力学の 薄膜干渉を説明します。 なにげない現象の中の不思議を感じ取っていただければ幸いです。
無反射膜での光の反射
「無反射膜」という言葉を聞いたことはありますか？ それは、光の反射率を小さくするために、ガラスにつける 薄い膜のことです。 最近の高級な時計にはついているようです。
なぜ、薄い膜が、光の反射率を小さくするのでしょうか？ 実は、これは、かなり不思議なことなのです。
私たちは光が粒子のように観測されることを知っています。 光が粒子のように観測されるのであれば、光は粒子のように飛んでいるはずです。 しかし光が粒のように飛んでいると考えると、 膜によって反射率が下がるという現象を説明することがとても難しくなるのです。
膜の表面がすべすべであることは、反射率が下がる理由ではありません。 膜の厚みが反射率を下げています。 膜の厚みがある一定の値のとき、反射率が格段に小さくなります。 これは膜の表面で反射した光の波と膜の裏側で反射した光の波が打ち消しあってしまうためです。 私たちは、その現象を干渉と呼びます。
光の粒子を 光子 と呼びます。 光子は膜の表面で反射したのでしょうか？ 光子は膜の裏側で反射したのでしょうか？ その干渉は1個の光子に対して起きるのです。 1個の光子が同一の場所、同一時刻で干渉するならば、 1個の光子が複数の時刻に出発する必要があります。 なぜならば、光子の速度は一定の光速度であるためです。
1個の光子は、複数の時刻に出発したのでしょうか？ 謎は深まるばかりです。
第10章シュレーディンガーの猫

ボーアのコペンハーゲン解釈

1927年にデンマークの物理学者ニールス・ボーアは 次のことを主張しました。
  • 一般的に物理系は測定されるまで明確な特性をもたない。
  • 量子力学は、測定がある結果を生成する確率を予言するだけである。
ニールス・ボーア研究所がデンマークのコペンハーゲンにあるため、 この主張はコペンハーゲン解釈と呼ばれています。 これは、量子力学の主流な解釈です。

フォン・ノイマン＝ウィグナー解釈

フォン・ノイマンとユージン・ウィグナーは1932年にコペンハーゲン解釈を拡張し、 次のことを主張しました。
  • 意識が波動関数の崩壊を起こす。
この主張はフォン・ノイマン＝ウィグナー解釈と呼ばれています。 オーストリアの物理学者エルヴィン・シュレーディンガーは、 この解釈には問題があると考えました。 そこで、彼は1935年に思考実験 「シュレーディンガーの猫」を提示しました。

シュレーディンガーの猫のパラドックス

箱の中に猫をいれます。 そして放射性同位体の崩壊の観測装置を置きます。 この観測装置を毒ガス噴出機に接続します。 放射性同位体が崩壊すると、観測装置が信号を毒ガス噴出機に送ります。 その結果、毒ガスが噴出し猫が死んでしまいます。
放射性同位体の崩壊現象は波動関数で記述されます。 つまり、放射性同位体の状態は、 崩壊した状態と、崩壊していない状態の、重ね合わせになります。 そのため、放射性同位体が崩壊したかどうかは観測するまでわかりません。
フォン・ノイマン＝ウィグナー解釈が正しいとすると、 人間の意識が波動関数の崩壊を起こします。 そのため、人間が観測するまでの間、猫は生死の重ね合わせになります。 この猫を、シュレーディンガーの猫、またはシュレデンガーの猫と呼びます。
猫の生死の重ね合わせは非常識だ。 したがって、フォン・ノイマン＝ウィグナー解釈は正しくない。 これが、シュレーディンガーの主張です。
フォン・ノイマン＝ウィグナー解釈は、コペンハーゲン解釈の拡張です。 シュレーディンガーは、 フォン・ノイマン＝ウィグナー解釈に反論するため、 シュレーディンガーの猫のパラドックスを提示しました。

シュレーディンガーの猫

シュレーディンガーの猫の解決策

コペンハーゲン解釈では、物理系は測定されるまで明確な特性をもちません。 測定されるまで猫の系は特性をもたないため、問題は存在しません。
一方、エヴェレットの多世界解釈では、生きている猫と死んでいる猫が 別の世界に存在します。 しかし多世界解釈が正しいことを示す実験的な証拠はまだありません。
結論として、この問題は論争が続いており未解決です。 今後の解決を待ちたいと思います。
第11章波動関数の不思議

波動関数とは粒子の観測確率を記述する関数です。 波動関数の物理的意味はなんでしょうか？ これを考えてみたいと思います。

波動関数の形

たとえば、1個の電子が飛んでいるとします。 直径1センチメートルぐらいのビー玉が飛んでいるところを思いうかべましたか？ その電子の状態は波動関数で記述できます。
右方向が電子の進行方向です。 上方向が虚数です。ななめ方向が実数です。 波動関数は複素数のため、それを表現するために3次元空間が必要となります。 多くの人は、複素数は「ありえないモノ」と思っているかもしれません。 しかし、絵で見ると普通の「らせん」です。
横軸からの距離が波動関数の高さです。波動関数の絶対値と呼ばれています。 横軸からの方向が波動関数の角度です。波動関数の位相と呼ばれています。
絵は電子が飛んでいるというイメージから程遠いですね。 絵をみても不思議さを感じない人がいるかもしれません。 しかし私は、大部分の人が次のように感じると思います。
「この絵はまったく電子に見えない」
そのように感じるのが、普通ふつうの感覚だと思います。

コペンハーゲン解釈かいしゃく

電子の半径は1フェムトメートルより小さいです。 1フェムトメートルは、10-15メートルです。 原子核かくの大きさは1フェムトメートルです。 電子は原子の大きさに広がっています。原子の半径は53,000フェムトメートルです。 原子核が半径1ミリメートルの球ならば、電子は半径53メートルの領域に広がっていることになります。 そして私たちは電子を1カ所で観測します。 これを波動関数の収縮といいます。
これは不思議なことだと思います。観測すると波は突然消えてしまうのでしょうか？ この不思議さを説明する考え方にコペンハーゲン解釈があります。 コペンハーゲン解釈は、この現象を次のように説明します。
  • 一般的に物理系は測定されるまで明確な特性をもたない。
  • 量子力学は、測定がある結果を生成する確率を予言するだけである。
このようにコペンハーゲン解釈の考え方はとても合理的です。 しかし、私の世界観からすると、この考え方には、不思議な感覚を覚えます。 たとえば、 「正しく動作しているiPhoneの中身を見たら…空だった！」 というような感覚です。

波動関数の物理的意味

波動関数の物理的意味とはなんでしょうか？ 波動関数はなにを表しているのでしょうか？
  • 波動関数は、世界の果てまで連続しています。 しかし、なぜ波動関数は途中で途切れないのでしょうか？
  • 波動関数の絶対値を定数倍しても、計算結果は変わりません。 しかし、波動関数の絶対値の物理的意味はなんでしょうか？
  • 波動関数の位相を一定角度回転させても、計算結果は変わりません。 しかし、波動関数の位相の物理的意味はなんでしょうか？
私たちは、3次元空間に生きています。 アインシュタインは、 「空間が、曲げることができる材質で、構成されていること」を 教えてくれました。 であれば、波動関数も曲げることができる材質で、構成されている可能性があります。 波動関数の絶対値は、空間の長さのようなものかもしれません。 波動関数の位相は、空間の角度のようなものかもしれません。

第11章量子力学のスピン

量子力学のスピンとは、電子のような小さな粒子の自転です。
私たちが日常的に飲む水は、水素原子と酸素原子からできています。 水素原子では、陽子のまわりを電子がまわっています。 原子はとても小さいので、想像するのがとても難しいです。 そこで、日常的に使う単位系で原子を表現したいと思います。 その単位系を「日常単位系」と呼びます。

電子の半径は390フェムトメートル(日常単位系:39センチメートル)です。 しかし、実際にはそれは正しくありません。 電子は1フェムトメートル(日常単位系:1ミリメートル)より小さいことが実験的に分かっているためです。
陽子と電子は自転しています。量子力学では、それをスピンと呼びます。 粒子はスピンの回転速度を速くすることもおそくすることもありません。 スピンの角運動量は固定です。
スピンを説明するため、ミュー粒子のスピンを考えます。 ミュー粒子は電子のような粒子です。 質量は106MeV(日常単位系:106g)、 寿命は2 マイクロ秒(日常単位系:7億年)です。 ミュー粒子は2個のニュートリノと1個の電子に崩壊します。

磁場がないならばスピンの回転軸は任意の方向をもちます。 電子の飛び出る方向からミュー粒子のスピンの回転軸の方向がわかります。 なぜなら、電子はミュー粒子のスピンの逆方向に飛び出るためです。
一方、磁場があるならば、スピンは二つの方向のみをもちます。 スピンの状態は磁場の方向と同じか反対方向です。 スピンの状態は、 スピンの方向が磁場と同じ状態と、 スピンの方向が磁場と反対の状態の重ね合わせです。 電子がミュー粒子から飛び出す方向はその二つだけです。 つまり、磁場は回転対称性を破ったのです。
多くの人はスピンを自転と考えていません。 なぜならば、次の二つの問題があるからです。
実験的に、電子の半径は、 1フェムトメートル(日常単位系:1ミリメートル)以下であることがわかっています。 スピンの角運動量を実現するには、 その回転速度は光速の390倍になります。 もしも電子の半径が390フェムトメートル(日常単位系:39センチメートル)ならば、 スピンの回転速度は光速になります。スピンを360度回転させると、波動関数の位相が逆になります。 スピンを720度回転させると、波動関数の元の位相に戻ります。 このため、スピンの波動関数は二価性をもちます。
上記の問題があるため、多くの人々はスピンを自転と考えていません。

 第12章多世界解釈 
多世界解釈とは量子力学の解釈の一つです。この解釈によれば、この世界
と異なるたくさんの世界が存在します。プリンストン大学の学生だったヒュー・エヴェレットは1957年に量子力学の新しい解釈を提唱しました。 その解釈はエヴェレットの多世界解釈と呼ばれています。
たとえば、箱の中に電子を入れます。量子力学によれば、電子は箱の中で波のように広がっています。 この波のことを波動関数といいます。 人間が箱の中を見れば、電子は箱の中の一点で見つかります。 これを波動関数の崩壊といいます。
電子は、常に粒子で、その存在確率が波にしたがっているだけではないか？ そのように考えるのは当然でしょう。しかし、その解釈は正しくありません。 アスペの実験が1982年にその解釈を否定しました。 観測する前の電子は、波のように広がっているのです。
この波動関数の崩壊は、とても不思議な現象です。 たとえば箱の中を、二つの部屋に仕切ります。 すると、電子の波はそれぞれの部屋に存在します。 片方の部屋を見れば、そこには電子はあるかもしれませんし、 ないかもしれません。
電子がある場所で見つかれば、電子の波動関数はその場所に収縮します。一方、電子が見つからなければ、 電子の波動関数は隣の部屋へ収縮します。 電子を観測した時に、その電子の波動関数が崩壊することはとても不思議です。 しかし、電子を観測しなかった時にも、 その電子の波動関数が崩壊するのはもっと不思議です。
エヴェレットは、「波動関数は崩壊していない」と考えました。 電子を波動関数で表現するのであれば、人間も波動関数で表現すべきだ。 ある人間が電子を観測すると、人間は次のように分かれます。
  1. 場所xで電子をみつけた人間A
  2. 場所yで電子をみつけた人間B
  3. 場所zで電子をみつけた人間C
電子は波のように広がっています。一方、人間も波のように広がっているのです。私が多世界解釈に初めて触れたのは ブルーバックス「宇宙の運命」でした。 読んだのは10歳くらいのころでしょうか？その本から引用してみましょう。しかし、SF作家がいうように、偶然が起こるたびに宇宙が二つに分かれると考えてみよう。 もしそれが事実ならたくさんの宇宙が存在しうる。 すこしちがった宇宙、かなり違った宇宙、思いつけるだけの宇宙が存在することになろう。こんな、幻想的な考えに、反証するのは簡単だろうと思われるかもしれない。 しかし、実はそうではない。 エベリット理論は量子力学の標準的な考え方と、数学的に同じなので、 この二つの違いを見分ける実験は不可能である。
これを初めて読んだ時には、とてもありえそうにないと思いました。 しかし、その後、大学時代に もしかすると正しいかも、と考えるようになってきました。
きっかけは、「CP対称性の破れ」の講義での「K中間子ミキシング」の話でした。 このK中間子ミキシングでは、K中間子と反K中間子を重ね合わせた波動関数が出てくるのです。
コペンハーゲン解釈では、物理系は測定されるまで明確な特性をもちません。 そのため、2種類の素粒子の重ね合わせは、測定されるまで明確な特性をもちません。
明らかに異なる2種類の素粒子の重ね合わせというものを理解するためには、 多世界解釈のような考え方がとても有効でした。
そのようなきっかけで、多世界解釈は正しいかもしれないと考えるようになりました。しかし、現在の多世界解釈の定式化では確率解釈を導出できないため、 その定式化には問題があると考えています。 多世界解釈の定式化は量子力学の数学的構造に依存ているため、 もし多世界解釈を採用するのであれば、その数学的構造にも拡張が必要。

 第13章時間の矢

私たちの身の回りを見わたしてみると、この世界には不可逆な現象が満ちています。未来方向の時間と過去方向の時間が明確に異なることはとても自然です。 しかし物理学的に考えるとこの考え方が異なってくるのです。物理学
的な時間の矢は 時間は過去方向も未来方向もほとんど変わらないのです。
たとえば2個のボールが衝突する様子を考えてみましょう。 二つのボールはたがいに接近した後、衝突して、はなれてゆきます。 この現象をビデオで撮影します。 この映像を逆向きに再生しても、物理法則に反するところはなにもありません。 すべての物理理論は、時間について対称なのです。
K中間子という素粒子の崩壊現象では時間対称性のずれが存在します。 しかし、日常的にみる過去と未来の時間方向のちがいを生み出すものではありません。
熱力学的には、熱力学第2法則というものがあります。 その法則は、乱雑さの度合を示すエントロピーという量が未来に向かって増大すると述べています。 これが過去と未来の非対称性の原因なのではないのと考える人もいるかもしれません。 しかし、これは経験則であり、なぜエントロピーが増大するかはよくわかっていません。
なぜ、時間は未来方向にしか流れないのでしょうか？ たとえば、この世界が映画のテープのような世界だと考えてみましょう。 すると、ひとつの疑問が生じます。 なぜこれほどまでに、二つの方向に非対称性が存在するのでしょうか？ 片方のはしにはビッグバンが存在し、もう片方向は、無限に続いています。多世界解釈と時間の矢の関係について私は次のように考えています。
多世界解釈では、異なる時間に属する世界は、多世界の一種とみなします。 また、多世界解釈では、映画のテープのようにひとつの歴史があるのではありません。 くもの巣のように、さまざまな歴史が広がっていきます。 各世界には、時刻というインデックスが割りふられるわけではありません。 各世界の差異のみが存在します。
たとえば、その世界の時計が時刻 t を指している世界を考えてみましょう。 この世界から遷移する世界は、可能性として、さまざまな世界が考えられます。 それらのほとんどの世界の時計では時刻 t + 1 を指していますが、 一部の世界では、 t - 1 を指しているかもしれません。
しかし、その世界の時計が時刻 t + 1 を指している世界が圧倒的に多いので、 私たちはほとんどの場合に時間の進行を観測します。 これが多世界解釈による時間の矢の説明です。 エントロピーの大きい世界は、エントロピーの小さい世界より多いので、 エントロピーの大きい世界へ遷移しやすいのです。


しかし、将来エントロピーが最大値を示したときに、 このような世界間の遷移が発生したとしても、時刻の進行は観測できないでしょう。 つまり、エントロピーが最大の世界では、正しく機能する時計は存在しないと考えています。
第14章多世界解釈について詳細

この世界を2次元の紙と仮定します。 私たちは、その紙の世界を、3次元の世界にたくさん置くことができます。 このように、次元が一つ増えるだけで、場所は大量に増えます。 そのような次元として時間があります。
 通常、私たちは、同時刻の世界を多世界のひとつと考えます。 しかし、10分後の世界も多世界にふくまれる世界のうちのひとつなのです。私たちは距離同様に時間を測定できるため、 時間も距離と同様に実在していると感じています。 時間は距離と同じようには存在しないと考えています。 実際には、時刻の異なる世界が複数存在していると考えています。 私たちは、時刻の異なる世界の間の遷移を時間の経過と感じているのです。
もし、宇宙が永遠に大きくなり続けるなら、時間は永遠に続く気がします。 しかし、エントロピー増大なしでは時間を測定できないと考えています。 遠い未来のエントロピー最大の世界では、時間の経過という現象は 存在しないと考えます。 エントロピーの最大近辺の個々の世界間で遷移は起こりますが、 時間が経過したようには見えません。 時間の矢の方向は、エントロピーが増大する間ははっきりしています。 しかし、エントロピー最大の世界では、はっきりしません。
世界の個数を無限と考えている人がいます。世界の個数は有限だと考えています。 もし、電子の位置を無限小の距離ずらせるならば、世界の個数は無限です。 なぜなら、電子の位置の異なる世界は別の世界であるためです。
最小距離と最小時間が存在すると考えます。 電子を無限に短い距離だけずらせないため、世界の個数は有限です。
世界の分岐でエネルギーが増えると考えている人がいます。 多世界の世界は、時刻の異なる世界と同じです。 私たちは、通常、エネルギー保存則を確認するために、 異なる時刻のエネルギーを足しません。 したがって、エネルギー保存則を確認するために、 異なる世界のエネルギーを合計する必要はありません。
多くの人が、ほかの世界は観測できないと考えています。 未来で、ほかの世界を観測できると信じます。 波動関数は実際には非線形と推測します。 その非線形性を利用してほかの世界を観測できるかもしれません。
非線形のアインシュタイン方程式の関数は空間の波を表現します。 波動関数は、私たちがまだ知らない新しい空間の波を表現していると推測します。 両方の関数が空間の波を表現しているため、波動関数は非線形かもしれません。経路積分と多世界解釈は密接な関係があると考えています。 問題点は、一意な基底を選ぶ方法がないことです。 それぞれの世界の状態は基底によって決まります。 もし一意な基底を選べないと、世界の状態を一意に決めることができません。

一意な基底を選ぶことができると考えています。 基底として、粒子りゅうしの位置を選ぶことができると考えます。 スピンに対する一意な基底を選ぶことができませんが、 スピンの内部空間の位置を基底として選べると推測します。

 第15章多世界解釈とボロン規則
多世界解釈には解決すべき問題があります。 その問題とは、ボルンの規則を多世界解釈で導出する方法が存在しないことです。 その問題を説明し、 ボルンの規則を導出するためのアイデアを紹介したいと思います。ボルンの規則
観測確率は波動関数の絶対値の2乗に比例します。 この事実は「ボルンの規則」と呼ばれています。 しかし、この規則は理論的に導かれたものではありません。 実験事実から導かれたものなのです。
多くの人は、この問題に興味がないようです。 それは教科書に基本原理として書かれているためかもしれません。 しかしながら、それは解決すべき重要な問題である。一部の人は多世界解釈でボルンの規則を導出できると考えています。 しかし、そのようには考えません。アメリカ人物理学者ヒュー・エヴェレットは1957年に多世界解釈を提唱しました。 彼は論文で、測度という新しい概念を導入しました。 測度は波動関数の絶対値の2乗に比例します。 彼は、測度が確率と同じように振る舞うと述べました。
彼は、測度が世界の個数に比例すると明言しませんでした。 しかし、多世界解釈を採用するのであれば、 世界の個数という概念を使用して確率を説明すべきと、考えます。
測度が世界の個数に比例するため、 測度は物理的実体として存在するはずです。 一方、波動関数は干渉するため、 波動関数が物理的実体として存在するはずです。
上記二つの物理的実体の関係を示すことが、 ボルンの規則を導出するための鍵だと、考えます。波動関数と測度の関係を示すアイデアを考えます。 一方、測度は波動関数の絶対値の2乗に比例します。 したがって、ある物理的実体の量と、その量の2乗が存在するアイデアを考えます。 アイデアを次に示します。
　ばねの長さと、ばねのエネルギー
　円の半径と、円の面積
　球の半径と、球の表面積
　点の個数と、各点間の経路の個数
1番目のアイデアでは、物理的実体としてばねが存在します。 波動関数の絶対値は、ばねの長さです。 世界の個数は、ばねのエネルギーに比例します。
2番目のアイデアでは、物理的実体として円が存在します。 波動関数の絶対値は円の半径です。 世界の個数は円の面積に比例します。
3番目のアイデアでは物理的実体として球が存在します。 波動関数の絶対値は球の半径です。 世界の個数は球の表面積に比例します。
4番目のアイデアでは物理的実体として点と経路が存在します。 波動関数の絶対値は点の個数です。 世界の個数は経路の本数です。３個の点に対して９本の経路があります。４番目の点と経路のアイデアが有力だと思っています。 
第16章重力と等価原理

アインシュタインは、1907年に等価原理をひらめきました。 等価原理とは、次の二つの状態が局所的に等価であるという原理です。等価原理によれば、私たちの周りの空間が、 重力加速度9.8[m/s2]で地球に向かって落ちていると解釈できます。等価原理の視点で重力が発生する仕組みを考えてみましょう。 重力加速度をニュートンの重力方程式で表現すると次のようになります。
g=GM/R2
重力加速度 g9.8[m/s2]
重力定数 G6.7×10-11[m3/s2kg]
地球の質量 M6.0×1024[kg]
地球の半径 R6400[km]
両辺に4πR2 をかけると次のようになります。
4πR2g = 4πGM
等価原理の視点では、地球が、半径 R の球殻で 4πR2×9.8[m3] の体積を加速的に吸い込んでいると解釈できます。 一方、右辺は4π×6.7×10-11×M [m3] の体積を 加速的に吸い込んでいると解釈できます。
私たちの空間は3次元であるため、この加速的な吸い込みは距離の逆2乗に比例して減衰します。アインシュタインは時空の曲がり(時空歪曲)で表現できることを見抜きました。 1915年に一般相対性理論が完成しました。
運動する物体が無重力状態の空間に静止していると解釈するならば、 運動する物体の軌跡は時空の曲がりと解釈できます。
一般相対性理論を説明するために、空間を表現した、湾曲したシートがよく使われます。 しかし、実際には、空間ではなく時空が歪曲しているのです。
時空歪曲と物質の関係を探るため、次のアインシュタインの重力方程式を見てみましょう。
Gμν=8πGTμν
左辺のGμνが幾何学的な量です。 右辺のTμνが物質的な量です。 式より、物質が時空を曲げていることがわかります。 アインシュタインはかつて、この式は調和がとれていないと不満をもらしたことがある。 建物にたとえてみれば左翼は美しい大理石作り、右翼は粗末な木造だというのである。 なぜならば、左辺の重力場は美しく単純な幾何学的原理に基づいているが、右辺は実に非常に複雑で 気まぐれに見えるからである。
この「左翼は大理石作り」「右翼は木造」という表現は象徴的だと思います。 おそらく、右辺も幾何学的な量で書くべきなのでしょう。 物質も幾何学的原理にもとづいて表現すべきなのだと思います。
重力の発生原因はなんでしょうか？ アインシュタインの重力方程式は、物質と時空歪曲の関係を教えてくれます。 しかし、物質が時空を曲げる原因は教えてくれません。 物質は、いったいどのようにして時空を曲げているのでしょうか？空間の小さな領域は、実際には、平均すれば平らな表面上の小さな丘に性質が似ている。 すなわち幾何学の通常の法則はそこでは役に立たない。曲がっている、もしくはゆがんでいるこの特性は空間の一部から別の部分へ波のように連続的に伝わる。空間の曲率の変動こそ、私たちが物体の運動と呼ぶ現象で実際に起きていることである。つまり、物質とは歪曲した空間なのかもしれません。 物質が歪曲した空間であれば、左辺も右辺も歪曲した空間となるため、 重力の発生原因を説明できるかもしれません。 最終的な結論として、重力の発生原因は謎です。

 第17章　量子力学の確率解釈導出

量子力学の確率解釈では、ある電子の波動関数は、その電子の観測確率をあらわすと解釈します。 量子力学の確率解釈はボルンの規則ともよばれます。ボルンの規則とは、電子のような小さな粒子の観測確率は、 その粒子の波動関数の絶対値の二乗に比例するという規則です。一般的にボルンの規則は、量子力学の基本原理だと考えられています。 基本原理とは、それ以上問うことのできない前提であることを意味します。 そのため、多くの人は、ボルンの規則を、別の基本原理から導出しようとは考えません。 なぜなら、確率をラプラスの確率論で計算すべきと考えるからです。 ラプラスの確率論とは、確率を計算するための理論です。 フランスの数学者ピエール＝シモン・ラプラスが1814年に論を提案しました。 たとえば、袋の中に赤い球が3個、青い球が2個入っているとします。その袋の中に手を入れて、球を取り出します。赤の球を取り出す確率はいくらでしょうか？ この確率はラプラスの確率論で計算できます。 ラプラスの確率論では、事象と素事象という概念を使います。事象とは出来事のことです。 素事象とは、それ以上分けることのできない事象のことです。 たとえば、赤い球を取り出すという事象Rは、次の三種類の事象に分けることができます。
  1. 球r-1を取り出す事象
  2. 球r-2を取り出す事象
  3. 球r-3を取り出す事象
「球r-1を取り出す事象」はそれ以上分けることができないため、素事象です。 ラプラスの確率論では、期待する素事象の個数を、すべての素事象の個数で割ることで、確率を計算します。 たとえば、赤い球を取り出す事象Rの確率は、3/5です。 なぜならば、期待する素事象の個数は3であり、すべての素事象の個数は5だからです。
ボルンの規則にもとづく確率の計算方法は、 ラプラスの確率論にもとづく計算方法と、まったく異なります。 ラプラスの確率論では、確率を素事象の個数の比で計算するのに、 なぜ、ボルンの規則では、確率は波動関数の絶対値の二乗で計算するのでしょうか？ この疑問を「量子力学の確率問題」と呼ぶことにします。 多世界解釈と確率論で、この確率問題の解法を考えます。 次の節では多世界解釈について説明します。多世界解釈では、世界のすべてを波動関数で表現します。 この「世界のすべてを表現する波動関数」に対する描像が、個人によって大きく異なります。 宇宙の波動関数を想像するには、一個の粒子の波動関数から始め、 徐々にその個数を増やしていく必要があります。
確率問題を考えるため、多粒子の波動関数を考えます。
k番目の素粒子の位置をrk=(xk,yk,zk),とすると多粒子の波動関数は次のようになります。
Ψ=Ψ(r1,r2,r3,⋯,rn)
この波動関数は、n 個の素粒子の位置を表現しています。 素粒子の配置を変えれば、あらゆる宇宙を構成できます。

多粒子の波動関数
多粒子の波動関数の一点が、一つの世界に対応します。 その確率分布P は次のようになります。
P(r1,r2,r3,⋯,rn)=|Ψ(r1,r2,r3,⋯,rn)|2確率論によるボルンの規則の導出
次の論文は、ボルンの規則を多世界解釈と確率論で導出します。
多世界解釈でボルンの規則を導出する際に、必要となった概念が次の階層宇宙という概念です。ここでは、階層宇宙の概略を説明しようと思います。
階層宇宙とは入れ子になった宇宙です。
我々の宇宙には粒子が存在します。そしてその粒子に対応する波動関数が存在します。 その波動関数の絶対値を半径とする小さな別の宇宙が存在すると考えます。
その小さな宇宙には粒子が存在します。そしてその粒子に対応する波動関数が存在します。 その波動関数の絶対値を半径とする、さらに小さな別の宇宙が存在すると考えます。
また、我々の宇宙の半径を絶対値とする波動関数が存在します。 その波動関数に対応する粒子が存在します。その粒子は、大きな別の宇宙に存在します。

つまり我々の宇宙と小さな宇宙は波動関数によって結ばれているのです。 仮にこの世界が12番目の宇宙ならば、小さな宇宙は13番目の宇宙です。 そして大きな宇宙は11番目の宇宙です。

 第18章宇宙とは


    「万物は数である」 ――― ピタゴラス (紀元前582年 - 紀元前496年)とある。
      また、ある人は
  • この世界は数字ではない。
  • 物理的世界が実在する。
  • 物理的世界を自由意思で改変できる。
だからずっと、次のようなことを考えていました。
  • この世界は、いつできたのか？
  • この世界は、どこにあるのか？
その後、ある人は考えを改めました。 この世界は数学的事実なのだと。 たとえるならば、次のような数学的事実です。
  • 5種類の正多面体が存在する。
  • 26種類の散在型単純群が存在する。
  • ゼータ関数の零点が一直線上に無限に存在する。
最大の散在型単純群はモンスター群と呼ばれています。
リーマン予想は証明されていませんが、 ハーディ(1914)および、ハーディとリトルウッド(1921)は、 Re(s) = 1/2上に零点が無限に存在することを示しました。 したがって、零点が一直線上に無限に存在することは数学的事実です。
物理学者スティーヴン・ワインバーグは1984年に次のように述べました。
宇宙は対称群の表現の巨大な直積だよ。これ以上、的確には言いあらわせないんじゃないかな。
ある人は、宇宙を26種類の散在型単純群の表現の直積だと推測します。
数学的事実は常に存在します。いつできたというものではありません。 数学的事実が存在するための時間は必要ありません。
数学的事実はどこにでも存在します。ある場所から動くようなことはありません。 数学的事実が存在するための場所は必要ありません。
宇宙が始まる前の、時間も空間も物質もない世界を想像してみましょう。 そこでは、いかなる物体が存在できるのでしょうか？ もしそこになにかが存在できるならば、それは数学的事実だけでしょう。
数学的事実ですから、その世界の外側から世界の内部を改変することはできません。 その数学的事実の中に「この世界は数学的事実」と認識する生命体がふくまれているのです。 なんと自己言及なのでしょうか？
最後に、 物理学者フリーマン・ダイソンが 1983年に書いた記事から引用して、終わりたいと思います。

私はひそかなる期待をもっている。 その期待を裏づけるいかなる事実も、ましてや、いかなる証拠はない。 しかし私は期待しているのだ。 21世紀のある日、物理学者たちが、 思いもよらない方法で宇宙の構造に組みこまれている、 モンスター群に遭遇することを。
第19章波動関数の幾何学的解釈による量子確率

量子論の確率的な予測は不思議な現象である。本論文は波動関数を幾何学的に解釈することで、この不思議な現象を解明する。
この結果は量子論と相対論の統一の可能性を示唆する。また、この結果は多世界解釈の妥当性を示唆する。
量子論の確率的な予測を提供する多世界解釈の理論は存在しない。量子論の確率的な予測を得るため、いくつかの仮説を立て、多世界解釈のための理論を構築する。その理論を多事象理論と呼ぶ。
     仮説

「無境界」仮説

位置x、時刻t、位相θのような物理量がいくつか存在している。これらの物理量を「位置的量」と呼ぶ。すべての位置的量は境界を持たず、有界閉集合と仮定する。

   「最小単位」仮説

すべての位置的量は共通の最小単位uを持つと仮定する。

     「波動空間」仮説

新しいもう一つの位置的量wを仮定する。その量の空間を波動空間と呼ぶ。この量は波動関数と関係する。

     「位相空間」仮説

メビウスの帯のような構造を持つ位相空間θ を仮定する。これは波動関数のスピンとの類似である。したがって、波動関数を次のように定義する。

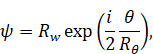ここで、Rwは波動空間の曲率半径である。また、Rθ は位相空間の曲率半径である。Rw、 Rθ と θは、変数θ、xと tの関数である。

    「素状態」仮説

状態の最小単位を仮定する。この状態を素状態と呼ぶ。例えば、量子論における一個の粒子の素状態を次のように表現する。



素状態は位置的量の組み合わせで指定できる。同一の素状態は、ただひとつだけであると仮定する。したがって、素状態は空間内の一点と解釈できる。ある一つの状態は、それらの点の集合と対応する。

     「素事象」仮説

ある一つの素状態から別のもう一つの素状態への遷移を素事象と呼ぶ。同一の素事象は、ただ一つだけであると仮定する。したがって、したがって、素事象は空間内の一本の線と解釈できる。ある一つの事象は、それらの線の集合と対応する。

すべての可能な素事象は存在する。これは経路積分との類似である。

      円環の構成

問題を簡単にするため、一個の粒子を考えよう。そして、w, θ ,x ,t を使用する。次のように円環を構成する。



そして、円環の表面上にある一点を次のように定義する。


Rw は波動関数のように、近似的な線形性を持つ。もしも円環の表面上に波が存在した場合、位相空間内における一周の効果と、二周の効果は相殺する。なぜならば、位相空間がメビウスの帯のような構造を持つからである。したがって、Rwは波動関数のような性質を持つ。

円環の形状は、その系のハミルトニアンHによって決定される。多数の粒子を記述するには、新しい位置的量を必要とする。これは第二量子化の類似である。

円環の表面上の一点は素状態f (w, θ, x, t)である。位置的量は最小単位を持つため、素状態は数えることができる。素状態の個数N (θ, x, t)を次のように計算する。

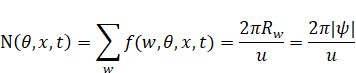(3.3)
ここで、u は最小単位であり、f (w, θ, x, t) = 1である。

      確率

量子論の確率とは、ある一つの事象の確率である。異なる素事象の個数だけを考察すればよい。なぜならば、我々は、多くの素事象のうちの、たった一つの素事象だけを観測するからである。

ここで、次の式を仮定する。


また、次の式を仮定する。



このとき、素状態の異なる組み合わせの個数としてm2を得る。なぜならば、時間が最小単位を持つからである。それらの組み合わせとは、素事象のことである。もしも、m個の異なる素状態が存在するならば、m2個の異なる素事象が存在する。


もしも、状態 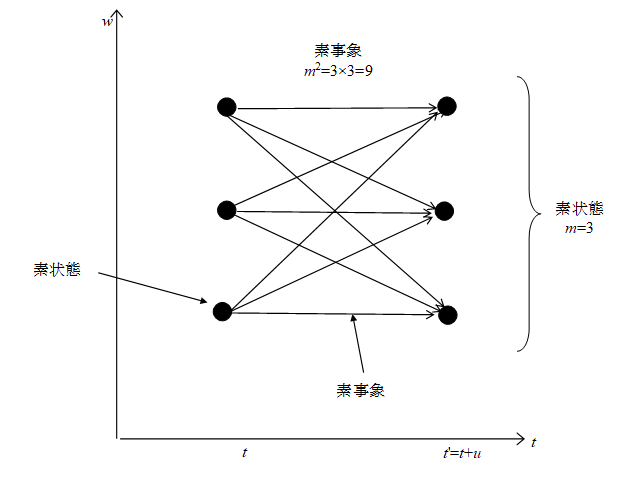 が存在するならば、位置xである一個の粒子を発見する確率P (x) は次のように表現できる。



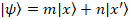したがって、この理論から確率を得ることができる。個々の素事象は存在する。したがって、個々の素事象を観測する観測者も存在する。この帰結は、多世界解釈である。

    結論

この理論は量子論の確率を提供する。 

第２０章多世界解釈と確率論によるボルンの規則の導出

ボルンの規則とは、電子のような小さな粒子を観測する確率が、波動関数の絶対値の2乗に比例するという規則である。多世界解釈でボルンの規則の導出を試みる。 
多くの研究者が多世界解釈でボルンの規則(ボルンの法則または確率解釈)の導出を試みてきた。しかし、誰も成功していない。このためボルンの規則の導出は多世界解釈の重要な課題となっていた。新しい方法として、量子論に確率論の素事象を導入し、ボルンの規則導出を試みる。

波動関数を三次元球面のような多様体とし、波動関数の絶対値を多様体の表面積とする。多様体が、格子点を持つ離散空間に存在すると仮定する。多様体の表面上の格子点をそれ以上分割できない状態、素状態とする。任意の点から任意の点へ矢印を引く。矢印をそれ以上分割できない事象、素事象とする。

確率は素事象の個数に比例し、素事象の個数は素状態の個数の2乗となる。素状態の個数は多様体の表面積に比例し、多様体の表面積は波動関数の絶対値である。したがって、確率は波動関数の絶対値の2乗に比例する。
２０．1       序論

２０．1.1      課題

ボルンの規則によると、粒子の観測確率は波動関数の絶対値の2乗に比例する。一方、多世界解釈によれば、さまざまな場所で粒子を観測した多くの事象が存在する。事象の個数を数えることでボルンの規則を導出することである。

２０．1.2      課題の重要性

波動関数の収縮とボルンの規則は量子力学の原理である。多世界解釈は、波動関数の収縮を量子力学から除いたが、ボルンの規則を除くことができなかった。
このため、多くの研究者がボルンの規則の導出を試みてきた。しかし、それらの試みは成功しなかった。このため、確率を導出することが重要な課題となっていた。

２０．1.3      これまでの導出方法

ヒュー・エヴェレット3世は1957年に、多世界解釈でボルンの規則が導出できると主張した。その後も多くの研究者がエヴェレットとは異なる方法で、ボルンの規則を導出したと主張してきた。ジェームズ・ハートルが1968年に、ブライス・ドウィットが1970年に、ニール・グラハムが1973年に主張している。
しかし、それらの導出方法には不十分な点があることをエイドリアン・ケントが1990年に指摘している。その後、デイヴィッド・ドイッチュが1999年にボルンの規則の導出を試みている。和田純夫氏も2007年にそれを試みた。しかし、研究者の間で合意の得られたボルンの規則の導出方法は存在していない。

２０．1.4  新しい導出方法

確率論では確率は根元事象(素事象)の概念で説明する。そのため、量子論の確率も同じ概念で説明できる可能性がある。そこで、新しい方法として、量子論に素事象の概念を導入しボルンの規則の導出を試みる。

２０．2       これまでの導出方法とその問題点

２０．2.1      ボルンの規則

マックス・ボルンは1926年にボルンの規則を提唱した。それは、ボルンの法則または確率解釈とも呼ばれている。ボルンの規則は量子力学の基本原理である。量子力学では、粒子の状態は波動関数ψ(x)で表現される。 
粒子の観測確率は波動関数の絶対値の2乗に比例する。位置 xにある粒子の観測確率 P(x) を次のように表現する。

(2.1)

量子力学の一般的な解釈であるコペンハーゲン解釈によれば、波動関数は物理的に実在しないため、観測前の粒子の状態には言及できない。しかし波動関数は物理的に実在している可能性がある。波動関数の実在を前提とする解釈の1つが多世界解釈である。

２０．2.2      エヴェレットの多世界解釈

エヴェレットは宇宙の波動関数を取り扱うため、1957年に多世界解釈を提唱した。彼は測度理論でボルンの規則の導出を試みた。

例として、シュテルン＝ゲルラッハの実験を考える。任意の方向のスピンの状態は、z軸上向きのスピンの状態とz軸下向きのスピンの状態の重ね合わせで表現できる。したがって、電子のスピンの状態ベクトルは、z軸方向のスピンの固有ベクトルで次のように表現できる。

(2.2)
係数a と ak は複素数である。

ここで、 |ψ> と |z+>, |z-> は規格化されている。

(2.3)

(2.4)

(2.5)

エヴェレットは確率を導出するため測度という新しい概念を導入した。彼は測度を正の関数 m (a) で表現した。この測度に対し、次の等式を要求する。

(2.6)
この要求を正当化する理由としてエヴェレットは確率保存則をあげている。この等式を満たす関数は、正の定数 c を用いて次のように書く。

(2.7)

(2.8)

(2.9)
上記の式は1957年にアンドリュー・グリーソンが一般的に証明している。その証明は『グリーソンの定理』と呼ばれている。エヴェレットは無限回の測定を考察し、測度が確率と同等にふるまうと結論した。しかし、エヴェレットの多世界解釈には基底問題と確率問題がある。それらについて次の節で説明する。

２０．2.2.1     多世界解釈の基底問題

ある特定の基底で測度を定義する場合、その特定の基底を選択する方法を示す必要がある。しかし、エヴェレットは、その論文で特定の基底を選択する方法を示さなかった。

例として、シュテルン＝ゲルラッハの実験を考える。
電子の波動関数を、z軸のスピンの固有状態の基底で、次のように表現する。

(2.10)
z軸のスピンの固有状態の測度は次のように表現できる。

(2.11)

(2.12)
一方、電子の波動関数を、x軸のスピンの固有状態の基底で、表現することもできる。

(2.13)
x軸のスピンの固有状態の測度は次のように表現できる。

(2.14)

(2.15)
もしエヴェレットの測度が物理的意味を持つ物理量ならば、固有状態の基底の選択で変化しないはずである。したがって、我々は特定の基底を選択する方法を必要とする。エヴェレットはその方法を示さなかった。

２０．2.2.2     多世界解釈の確率問題

エヴェレットは、測度理論でボルンの規則の導出を試みた。その際、エヴェレットは測度に物理的な意味を与えなかった。しかし、測度の等式に対し確率保存則を要求することは、測度を確率と定義することと同値である。そのため無限回の測定で測度が確率として振る舞うことを示すことは循環論法となっている。

もし世界の個数が測度に比例するならば、世界の個数が測度に比例する仕組みを明らかにする必要がある。もし世界の個数が測度に比例しないならば、世界の出現確率が測度に比例する仕組みを説明する必要がある。

２０．３       これまでの考え方の確認

２０．3.1      ホイーラーとデウィットの宇宙波動関数

ジョン・ホイーラーとブライス・デウィットは、1967年に宇宙波動関数を提唱した。その波動関数はハミルトニアン演算子 H とケットベクトル |ψ> を用いて次のように表現される。


(3.1)


このケットベクトル |ψ> は通常の関数ではなく汎関数である。

汎関数は数学的には多変数関数とほとんど同等である。汎関数での議論は難しいため、多変数関数で議論する。次の節で、多変数関数である多粒子波動関数について説明する。

２０．3.2      バーバーの宇宙の多粒子波動関数

ジュリアン・バーバーは1999年に著書『時間の終焉』で宇宙を多粒子系の波動関数(多粒子波動関数)で表現した。宇宙に素粒子がn個あり、k番目の素粒子の位置を rk = (xk, yk, zk ) とする。このとき、多粒子波動関数ψは次のように表現される。

(3.2)

多粒子の位置を表現した多次元空間を配位空間と呼ぶ。配位空間の一点は、すべての粒子の位置を表現するため、配位空間は過去、現在、未来の物理的に可能なすべての世界を表現する。別の言い方をすれば、多粒子波動関数は、多世界解釈におけるすべての可能な世界を表現する。ある世界のすべての粒子の配置が決まれば、その世界の時計の状態が決まる。その世界の時計の状態が決まれば、その世界の時計の時刻が決まる。そのため、多粒子波動関数の引数に時刻は不要となる。波動関数の基底として位置または運動量を選択できる。位置を基本的な基底として選択する。なぜなら、常に我々は実験で最終的に位置を観測するからである。場の量子論では粒子数が変化する。このため多粒子波動関数は量子場を表現できない。量子場を表現するため、汎関数を必要とする。一方、汎関数は多変数関数で近似的に表現できる。そこで、多変数関数である多粒子波動関数を使用する。配位空間内で、それぞれの世界を観測する確率 P を次の式で表現する。 

(3.3)

確率がこの式で表現される理由を考察するため、次節では確率論の考え方を確認する。

２０．3.3      ラプラスの確率論

ピエール＝シモン・ラプラスは1814年に古典的確率論をまとめた。彼は次のような、確率の計算方法を示した。任意の一つの場合が他の場合よりも頻繁に起きると推論させる事実が存在しない時、すなわち、任意の一つの場合が同様に確からしい時、期待する事象の確率は、期待する事象に都合のよい場合の個数と、可能なすべての場合の個数の比となる。この「同様に確からしい」場合が、確率論における素事象である。すべての素事象の発生確率は等しい。 
素事象は根元事象とも呼ばれる。すべての素事象の個数を Na とし、ある事象の素事象の個数を N とする。このとき、その事象の発生確率 P は次の式で表現される。 

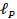(3.4)

(3.5)

たとえば、袋に5個の玉が入っているとする。5個のうち3個を赤玉、2個を青玉とする。赤い玉を取り出す事象の確率をPとする。このとき、確率Pは3/5となる。この理由は素事象の概念を用いて説明される。確率論では、個々の玉を取り出す事象が素事象である。事象は素事象の集合と解釈する。ボルンの規則を導出するためには、量子論における素事象を発見する必要がある。確率論の素事象は一般に、それ以上分けることができないため、量子論の素事象もそれ以上分けることができないことが期待される。 

２０．3.4      ペンローズのスピンネットワーク

ロジャー・ペンローズは1971年にスピンネットワークを提唱した。スピンネットワークでは、時空は離散的であり、空間は点と点を線で結んだグラフで表現される。このグラフはスピンネットワークと呼ばれる。時空が離散的であるため、時空は最小距離と最小時間を持つ。スピンネットワークは利用しないが、この理論と同様に時空が離散的すなわち不連続であることと、空間が点と点を線で結んだグラフであることを仮定する。最小距離をプランク長 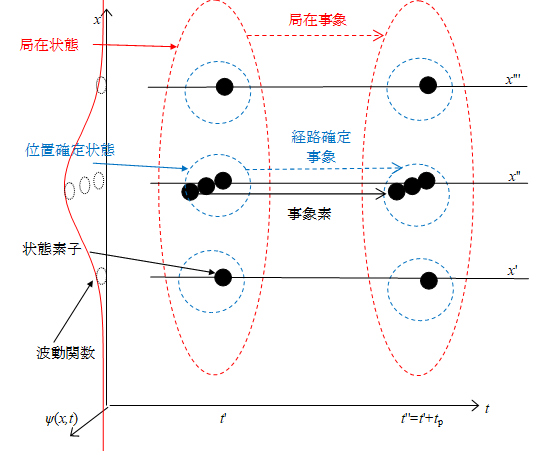 と仮定する。また最小時間をプランク時間 tP と仮定する。


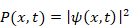(3.6)

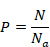(3.7)

プランク長で構成した最小の領域を素領域と呼ぶこととする。時空が不連続であれば、連続な時空を前提に構築していた理論を再検討する必要がある。そこで、次節では、経路積分が不連続な時空でどうなるかについて再検討する。

２０．3.5      ファインマンの経路積分

リチャード・ファインマンは1948年に経路積分を提唱した。経路積分は新しい量子化方法を提供する。経路積分では、粒子が取りうるすべての経路の和を取る。位置aから位置bへの確率振幅K(b, a)は次のように表現される。


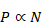(3.8)

確率振幅K(b, a)は伝播関数(プロパゲータ)と呼ばれている。記号Dx(t) はすべての経路に対する確率振幅の和を表現している。波動関数は伝播関数で次のように表現される。


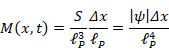(3.9)

経路積分では粒子が位置 a から位置 b に移動する事象を伝播関数 K(b, a) に対応させている。時刻taの波動関数に伝播関数 K(b, a) を乗じ積分することで、時刻 tb の波動関数を求める。

経路積分では、普通の経路 α のようなものだけでなく、短時間に長距離を移動する経路 β も存在する。このような経路は、光速を超えることもある。そのためこのような経路は、特殊相対性理論に反するため許されない。一般に経路積分では、次のように説明している。経路 α に近い微小に異なる経路の和は大きくなる。一方、経路 β に近い微小に異なる経路の和は小さくなる。このため、長距離遷移は抑制され、経路 β は残らない。それでは、最小時間 tP 後の場合には、何が起こるだろうか？位置 a から位置 b までの最小時間 tP 後の伝播関数 K(b, a)は次のように表現する。


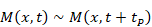(3.10)

時間の不連続性を仮定している。最小時間は、それ以上分割できないため、出発地点と到着地点が決まっている場合には微小に異なる経路を取ることができない。このため、長距離遷移は抑制されず、経路βは残る。したがって、もし、離散時空に経路積分を適用し、粒子の位置がディラックのデルタ関数のように決定されていたら、最小時間tP秒後に長距離遷移が生じる。


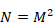(3.11)

しかし、実際に長距離遷移を観測することはない。この理由は、粒子の位置が正規分布で分布しているためであると推論する。そのため、位置xは、偏差Δxで分布し、運動量pも偏差Δpで分布する。不確定性原理によりΔxとΔpの積はプランク定数 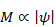 に近い。


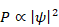(3.12)

運動量pを持つ粒子の波動関数は次のように表現できる。

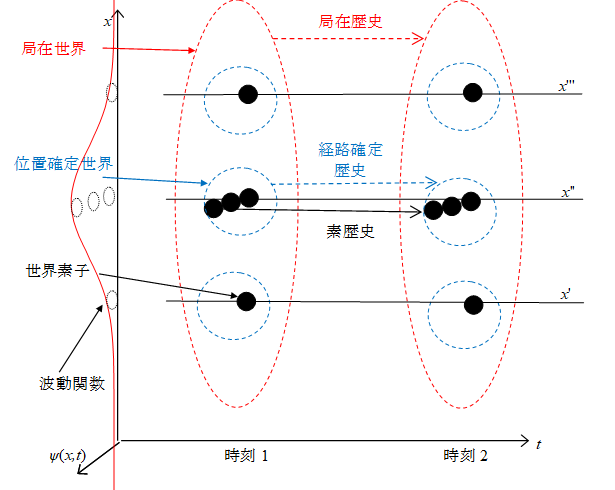(3.13)
この粒子の質量をm、速度をvとする。その運動量は次のとおり。

(3.14)
この式を波動関数に代入すると次の式を得る。

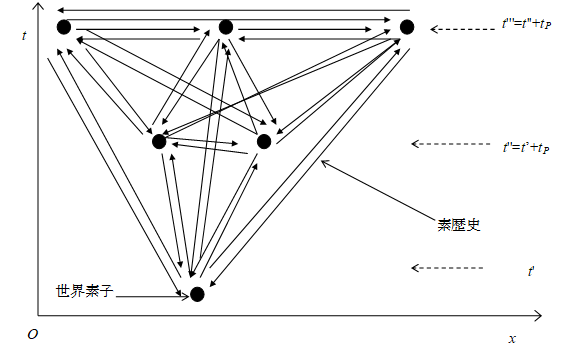(3.15)
速度vは、移動距離xとプランク時間tPで次のように表現できる。

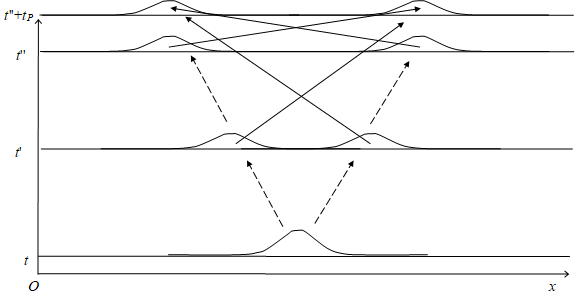(3.16)
この式を波動関数に代入すると次の式を得る。

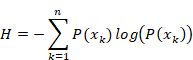(3.17)
上記の式より、短距離において波動関数の波長は長い。一方、長距離において波動関数の波長は短い。

そのため、短距離では、局在状態の経路積分の和は大きくなる。一方、長距離では、局在状態の経路積分の和は小さくなる。局在状態では、最小時間tP秒後に長距離遷移は発生しない。そのため、局在状態は、tP秒後も近くに局在している。このため、次の図のような経路積分の網目構造が実現していると推論する。状態Aから状態Bへ遷移する事象ABがあるとする。状態Aに位置が3個あり、状態Bに位置が3個あれば、事象ABには経路が3 × 3 = 9本ある。

「経路積分の網目構造」では経路の本数は位置の個数の2乗となる。一方、ボルンの規則によれば、確率は波動関数の絶対値の2乗となる。これらの2乗の類似性を議論する。

２０．3.6      ディラックの場の量子論

ポール・ディラックは、電磁波の放射と吸収を説明するため、1927年に場の量子論を提唱した。1次元の場合、場の量子論の基本交換関係は次のように表現される。


(3.18)

ここでψは場であり、 π は場 ψ の共役な演算子である。変数 x, y は位置、関数 δ はディラックのデルタ関数である。
この交換関係は、次の位置 x と運動量 p の交換関係と似ている。


(3.19)

このことは、場ψが位置xと同様に位置的な性質を持つ物理量であることを示唆する。位置 x に対する第一量子化によって場 ψ(x) を得た。一方、場ψは位置xのような「位置的物理量」である。このため、場 ψ(x) に対する第二量子化によって新しい場 Ψ(x, ψ(x)) を得る。 

第二波動関数Ψ(x, ψ(x))は、汎関数Φ[ψ(x)] と解釈できる。汎関数Φ[ψ(x)]は多粒子波動関数 ψ (x1, x2, x3, …, xn) で近似できる。簡単に議論するため、多粒子波動関数を使用する。

２０．3.7      カルツァ＝クライン理論

テオドール・カルツァは1921年に、オスカル・クラインは1926年に、重力と電磁気力を統一するため、1次元の円のような余剰空間を提唱した。この理論は、カルツァ＝クライン理論と呼ばれている。
通常の4次元時空M4と1次元の円状の余剰空間S1で、新しい時空M4×S1を次のように表現する。


(3.20)
 ２０．3.8      オイラーの公式
オイラーは1748年に次の公式を発表した。
(オイラーの公式)

(3.21)
虚数iは次の式を満たす。

(3.22)
複素数を次のように表現する。

(3.23)

(3.24)
複素共役を次のように表現する。

(3.25)
複素関数を次のように表現する。

(3.26)
複素数の絶対値の二乗は次のように表現できる。

(3.27)
次の記号を用いる。

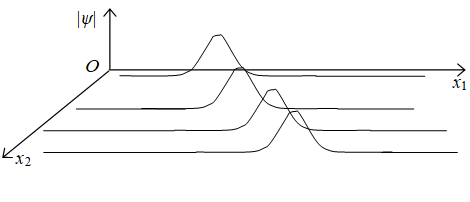(3.28)

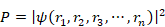(3.29)



２０．3.9      コーシー＝リーマンの方程式

オーギュスタン＝ルイ・コーシーは1814年に複素解析のため次の方程式を導入した。1851年にリーマンも複素解析のために、この方程式を利用した。
(コーシー＝リーマンの方程式)

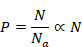(3.30)
上記の公式を次のように短く表現する。
(コーシー＝リーマンの方程式)

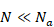(3.31)

コーシーは、次の公式を導入した。
(コーシーの積分公式)

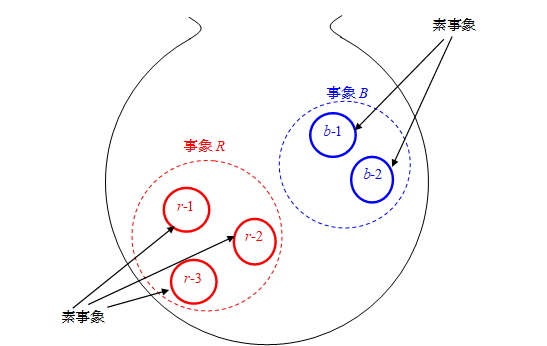(3.32)
S は周回経路である。

２０．3.10   ハミルトンの四元数

ウィリアム・ローワン・ハミルトンは、1843年に四元数を発表した。

(3.33)
四元数を次のように表現する。

(3.34)

(3.35)
四元数共役を次のように表現する。

(3.36)
四元数関数を次のように表現する。

(3.37)
四元数の絶対値の二乗を次のように表現する。

(3.38)

次の記号を用いる。

(3.39)

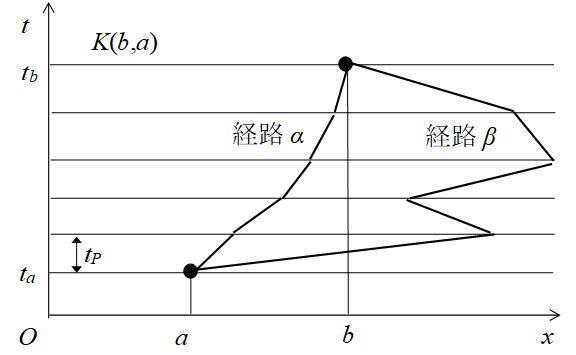(3.40)

２０．3.11   コーシー＝リーマン＝フューターの方程式

フューターは1934年に、四元数解析のため次の方程式を導入した。
(コーシー＝リーマン＝フューターの方程式)

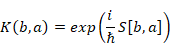(3.41)
上記の公式を次のように短く表現する。
(コーシー＝リーマン＝フューターの方程式)

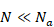(3.42)

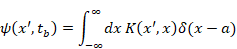(3.43)


フューターは、次の公式を導入した。
(コーシー＝フューターの積分公式)

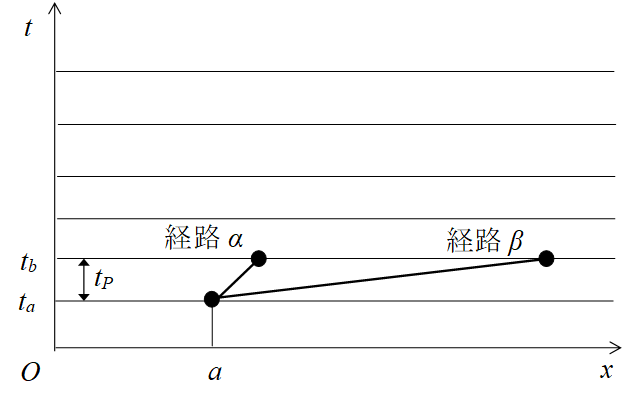(3.44)
ここで、S3 は3次元閉曲面である。四元数解析の詳細は、1979年のアンソニー・サドベリーの論文に記載されている。

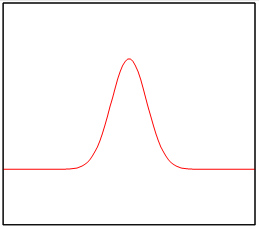
次の公式を使用する。
(四元数の積分公式)

(3.45)
ここで、uは単位四元数である。

２０．3.12   カルタンの微分形式
エリ・カルタンは、座標に依存しない方法で多様体を記述するため、1899年に微分形式を定義した。
微分形式 dω は無限小だが、有限小の差分形式 δω を用いる。

多様体 S の表面積 A を次のように表現する。

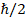(3.46)
多様体 S の差分形式 δS を次のように表現する。

(3.47)


ここで、多様体S1の差分形式δS1を次のように表現する。

(3.48)

また、別の多様体S2の差分形式δS2を次のように表現する。

(3.49)

多様体S1とS2の重ね合わせとして多様体Sを得る。

(3.50)

波動関数の重ねあわせでは、位置ごとに波動関数の複素数を加算している。そのため、多様体の重ねあわせでは、立体角ごとに表面積を加算すると推測する。

そこで、多様体Sの差分形式δSを次のように表現する。

(3.51)
したがって、球面調和関数に対し次の式が成立する。

(3.52)
上記の式で多様体の重ねあわせを定義する。
２０．４章       新しい導出方法

２０．4.1      2次元時空の宇宙

4.1.1     2次元時空の閉じた経路

2次元時空の宇宙 U を考える。

粒子の世界線 s を複素数で、次のように表現する。

(4.1)

(4.2)
この粒子の波動関数を次のように表現する。

(4.3)
この粒子が対生成し対消滅したとする。この閉じた経路sを半径rの円Cで次のように表現する。この閉経路Cは次のように表現できる。

(4.4)
この閉経路Cの周長 a は次のように表現できる。

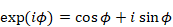(4.5)


(4.6)

(4.7)
閉経路Cは次のように表現できる。

(4.8)
すると、周長aは次のように表現できる。

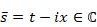(4.9)
周長aの差分形式を次のように表現する。

(4.10)

２０．4.1.2     波動関数の絶対値の導入

カルツァ＝クライン理論と同様に余剰空間として円Sを導入する。

円S上の点を複素数の行列表現で次のように表現する。

(4.11)

(4.12)

(4.13)

(4.14)
振幅1次元球面Sの周長 A は半径Rと複素立体角 Ω で次のように表現できる。

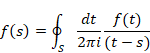(4.15)
半径Rがrとω の関数ならば、周長 A もrと ω の関数となる。

(4.16)
球面Sの差分形式δSで次のように表現する。

(4.17)
周長 A を波動関数の絶対値と解釈する。

(4.18)

２０．4.1.3     波動関数の位相の導入

波動関数の位相を導入するため、この球面を回転角度 Φ で回転する。ω に依存する回転変換 P で球面 S を球面 S’ に変換する。

(4.19)
ω に依存する回転角度 Φ の回転変換を次のように定義する。

(4.20)
関数 Φ (ω)を自然数nで次のように表現する。

(4.21)
この回転角度 Φ を波動関数の位相と解釈する。

(4.22)

回転変換で球面Sの差分形式を次のように変換する。

(4.23)

球面S1と球面S2の重ね合わせを次のように定義する。

(4.24)
球面と、180度回転した球面の重ね合わせは0になる。

(4.25)

(4.26)

粒子の閉経路Cと球面Sの直積は円環(トーラス) Tとなる。

(4.27)

(4.28)

(4.29)
ここで、次の新しい立体角νを導入する。

(4.30)
ここで、次の新しい半径ρを導入する。

(4.31)
ここで、次の新しい関数f (ρ, ν) を導入する。

(4.32)
この関数 f (ρ, ν) を使って、円環世界面Tを次のように表現する。

(4.33)
次の図のように、円環世界面は螺旋円環のようにねじれている。

この円環世界面の次元は、宇宙の次元と同じである。なぜなら、本節の宇宙は2次元時空だからである。

ここで驚くべきアイデアを使う。

この円環世界面を新しい時空と解釈する。この円環時空を一つの独立した宇宙とみなす。第二宇宙に、本節と同様の議論を適用することで、第三、第四の宇宙を構成できる。 

２０．4.1.4     階層宇宙 

階層宇宙を次の記号で表現する。

(4.34)


２０．4.1.5     方程式

位置sを複素数で次のように表現する。

(4.35)
すると波動関数は複素関数となる。

(4.36)
この複素関数を解析関数と仮定する。
解析関数はコーシー＝リーマンの方程式を満たす。

(コーシー＝リーマンの方程式)

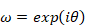(4.37)
共役を次のように定義する。

(4.38)
すると、経路微分方程式は次のように短く書ける。

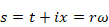(4.39)
解析関数はコーシーの積分公式を満たす。
(コーシーの積分公式)

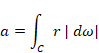(4.40)
S は周回経路である。
円S上の粒子が、位置tから位置sまで直接、長距離遷移すると解釈する。
各宇宙の波動関数は複素関数である。したがって、これらの方程式は、各宇宙の波動関数に適用できる。